8月7日までに一通り仕上げた後，夏休み課題を2往復目に突入・・・。その間，オリジナル単語帳（1400語程度）を手作りして単語の暗記方法も伝授！，さらに本文和訳からの本文英作という手法も伝授！，一先ずここまでは順調ですが引き続き油断することなく手元の課題に注力します。夏休み明けテストに挑みます。
岡山白陵の英語を大至急で対応。受験塾家庭教師
カテゴリー: 18.中学生諸君へ
【第2学区】三田市や丹波篠山市や丹波市など各高校における偏差値と内申点と定員割れ状況
兵庫県公立高等学校【第2学区】尼崎市 西宮市 伊丹市 宝塚市 川西市 猪名川町 三田市 丹波篠山市 丹波市
・兵庫県立北摂三田高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立柏原高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立三田祥雲館高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立篠山鳳鳴高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立三田西陵高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立有馬高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立篠山産業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立篠山東雲高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立氷上高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立氷上西高等学校の偏差値と内申点と定員割れ状況をだしてみた。
偏差値の算出方法（受験塾家庭教師による暫定）
内申点の算出方法（受験塾家庭教師による暫定）
・兵庫県公立高等学校【第2学区】尼崎市 西宮市 伊丹市 宝塚市 川西市 三田市 猪名川町 丹波篠山市 丹波市
・【第2学区】三田市や丹波篠山市や丹波市など各高校における偏差値と内申点と定員割れ状況
・【第2学区】西宮市など各高校における偏差値と内申点と定員割れ状況
・【第2学区】宝塚市や川西市や伊丹市など各高校における偏差値と内申点と定員割れ状況
・【第2学区】尼崎市など各高校における偏差値と内申点と定員割れ状況
・兵庫県公立高等学校（全日制・定時制・多部制・通信制）
・兵庫県にある各学区の各高校における偏差値と内申点と定員割れ状況
・直近のテストから志望校の合格最低点と自分の学力（偏差値と内申点）を知る。
・定員割れ公立高校の合格ラインは偏差値38で内申点80【兵庫県】
・過去10年分の定員割れ状況と兵庫県公立高等学校入学者選抜等
・複数志願選抜を知っとこ。【兵庫県公立高等学校入学者選抜より】
・兵庫県公立高等学校（定時制・多部制・通信制）の偏差値と内申点と定員割れ状況
・3年で卒業できる3修制がある兵庫県公立高等学校（定時制・多部制・通信制）
神戸市を拠点とする受験塾家庭教師オフィス神戸は【第2学区】に対応します。
三田市を拠点とする受験塾家庭教師オフィス三田は【第2学区】に対応します。
【第3学区】加古川市や高砂市など各高校における偏差値と内申点と定員割れ状況
兵庫県公立高等学校【第3学区】明石市 加古川市 高砂市 稲美町 播磨町 西脇市 三木市 小野市 加西市 加東市 多可町
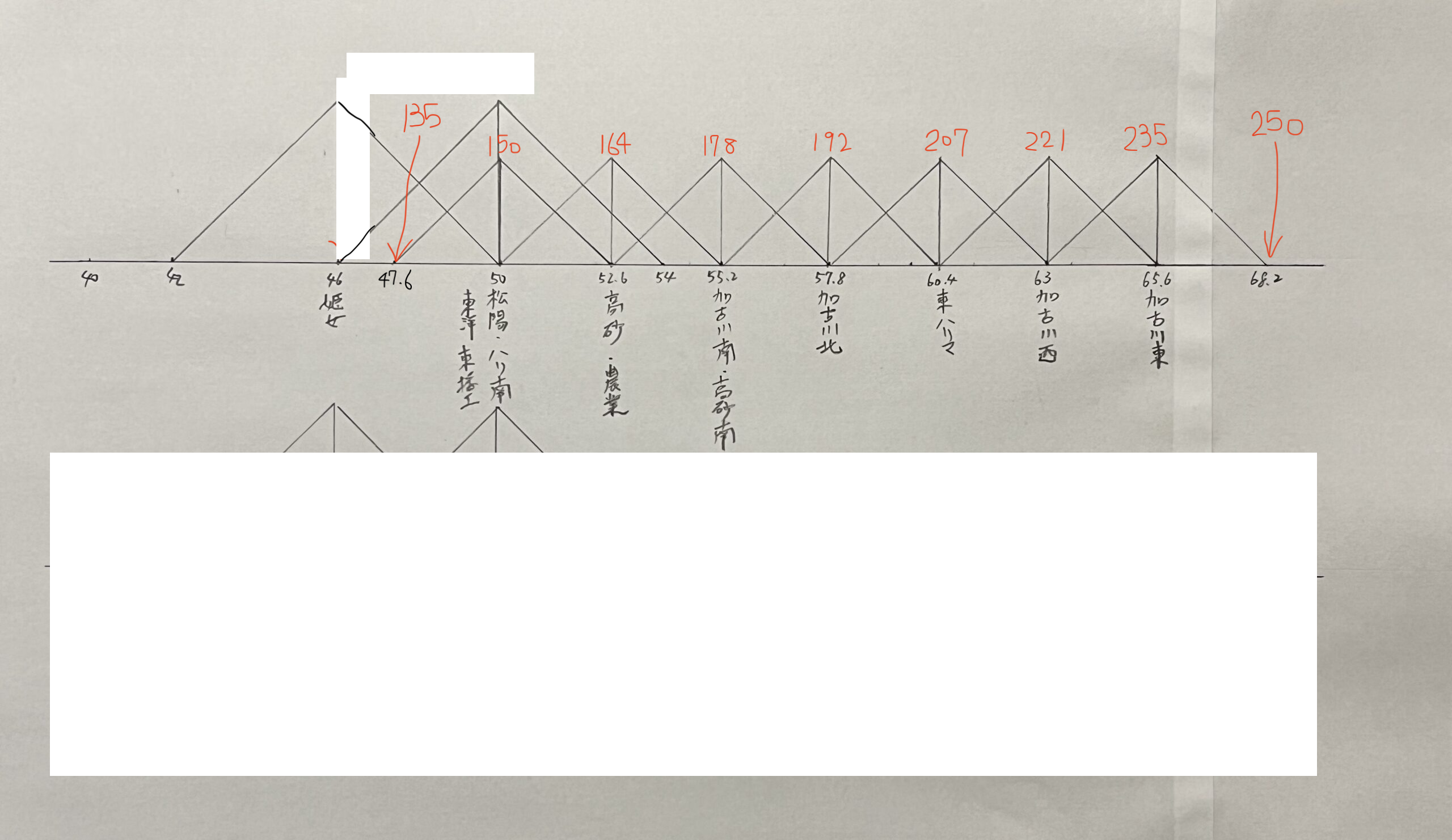
・兵庫県立加古川東高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立加古川西高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立東播磨高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立加古川北高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立高砂南高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立加古川南高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立高砂高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立松陽高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立農業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立播磨南高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立東播工業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
偏差値の算出方法（受験塾家庭教師による暫定）
内申点の算出方法（受験塾家庭教師による暫定）
・兵庫県公立高等学校【第3学区】明石市 加古川市 高砂市 西脇市 三木市 小野市 加西市 加東市 稲美町 播磨町 多可町
・【第3学区】加古川市や高砂市など各高校における偏差値と内申点と定員割れ状況
・【第3学区】明石市など各高校における偏差値と内申点と定員割れ状況
・【第3学区】小野市や三木市や西脇市や加東市や加西市など各高校における偏差値と内申点と定員割れ状況
・兵庫県公立高等学校（全日制・定時制・多部制・通信制）
・兵庫県にある各学区の各高校における偏差値と内申点と定員割れ状況
・直近のテストから志望校の合格最低点と自分の学力（偏差値と内申点）を知る。
・定員割れ公立高校の合格ラインは偏差値38で内申点80【兵庫県】
・過去10年分の定員割れ状況と兵庫県公立高等学校入学者選抜等
・複数志願選抜を知っとこ。【兵庫県公立高等学校入学者選抜より】
・兵庫県公立高等学校（定時制・多部制・通信制）の偏差値と内申点と定員割れ状況
・3年で卒業できる3修制がある兵庫県公立高等学校（定時制・多部制・通信制）
神戸市を拠点とする受験塾家庭教師オフィス神戸は【第3学区】に対応します。
三田市を拠点とする受験塾家庭教師オフィス三田は【第3学区】に対応します。
姫路市を拠点とする受験塾家庭教師オフィス姫路は【第3学区】に対応します。
加古川市を拠点とする受験塾家庭教師オフィス加古川は【第3学区】に対応します。
私立中高一貫校専門ってことでもないけど対応できるのが当たり前だから受験塾家庭教師
【 対応可能とする私立中高一貫校 】
・2003年からの合格実績（国公立大学）
・2003年からの合格実績（私立大学）
・2010年からの合格実績（医学部医学科）
・2003年からの合格実績（国公立高校）
・2003年からの合格実績（私立高校）
・2003年からの合格実績（私立中学校）
・2009年からの合格実績（私立小学校）
私立中高一貫校に通う妹ちゃんとお姉ちゃんと和田先生が６時間ぶっ続けで特訓
神戸市の中学生と高校受験生が絶対に理解するべき偏差値ならびに内申点
【第3学区】小野市や三木市や西脇市や加東市や加西市など各高校における偏差値と内申点と定員割れ状況
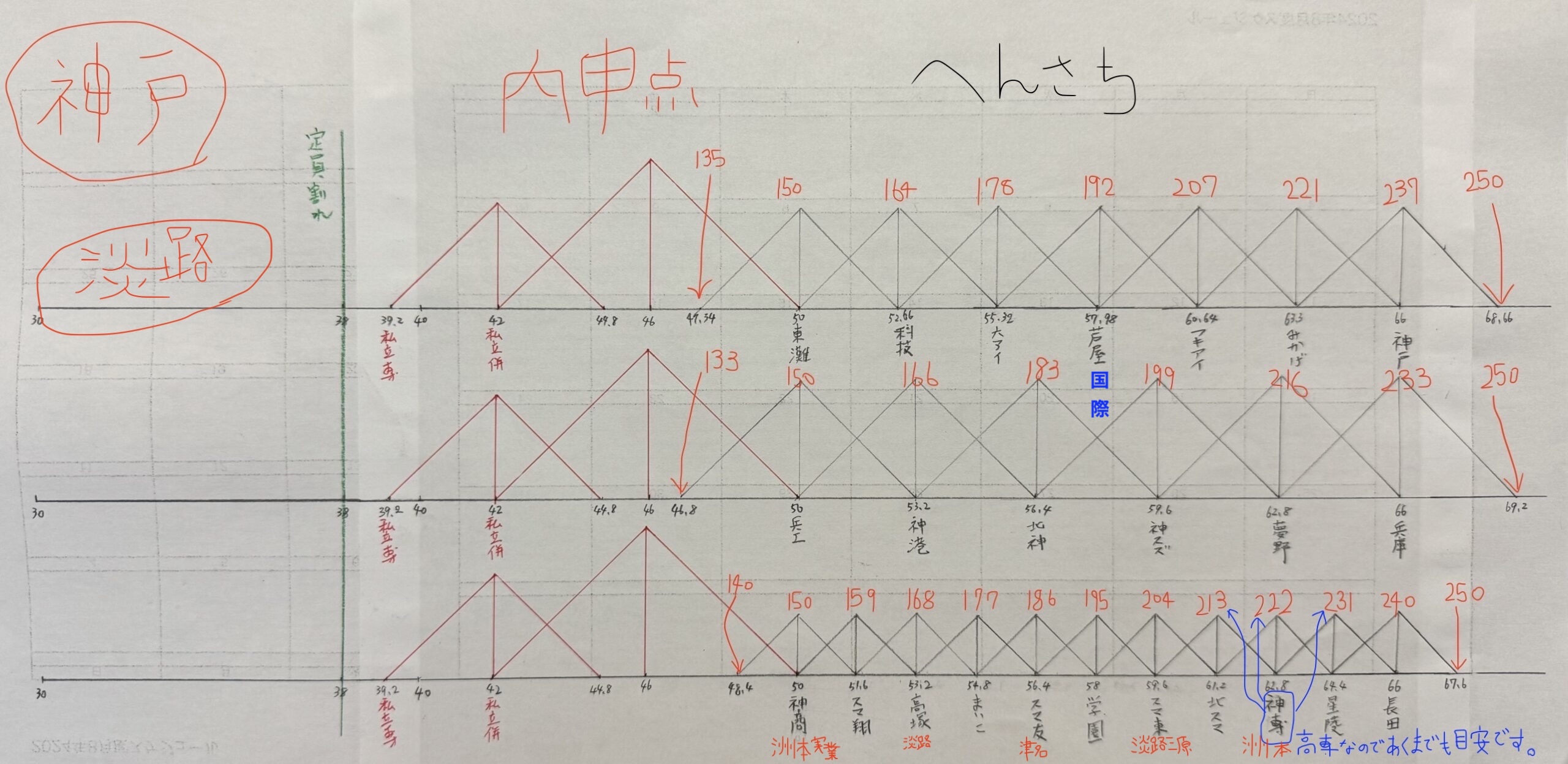
兵庫県公立高等学校【第3学区】明石市 加古川市 高砂市 稲美町 播磨町 西脇市 三木市 小野市 加西市 加東市 多可町
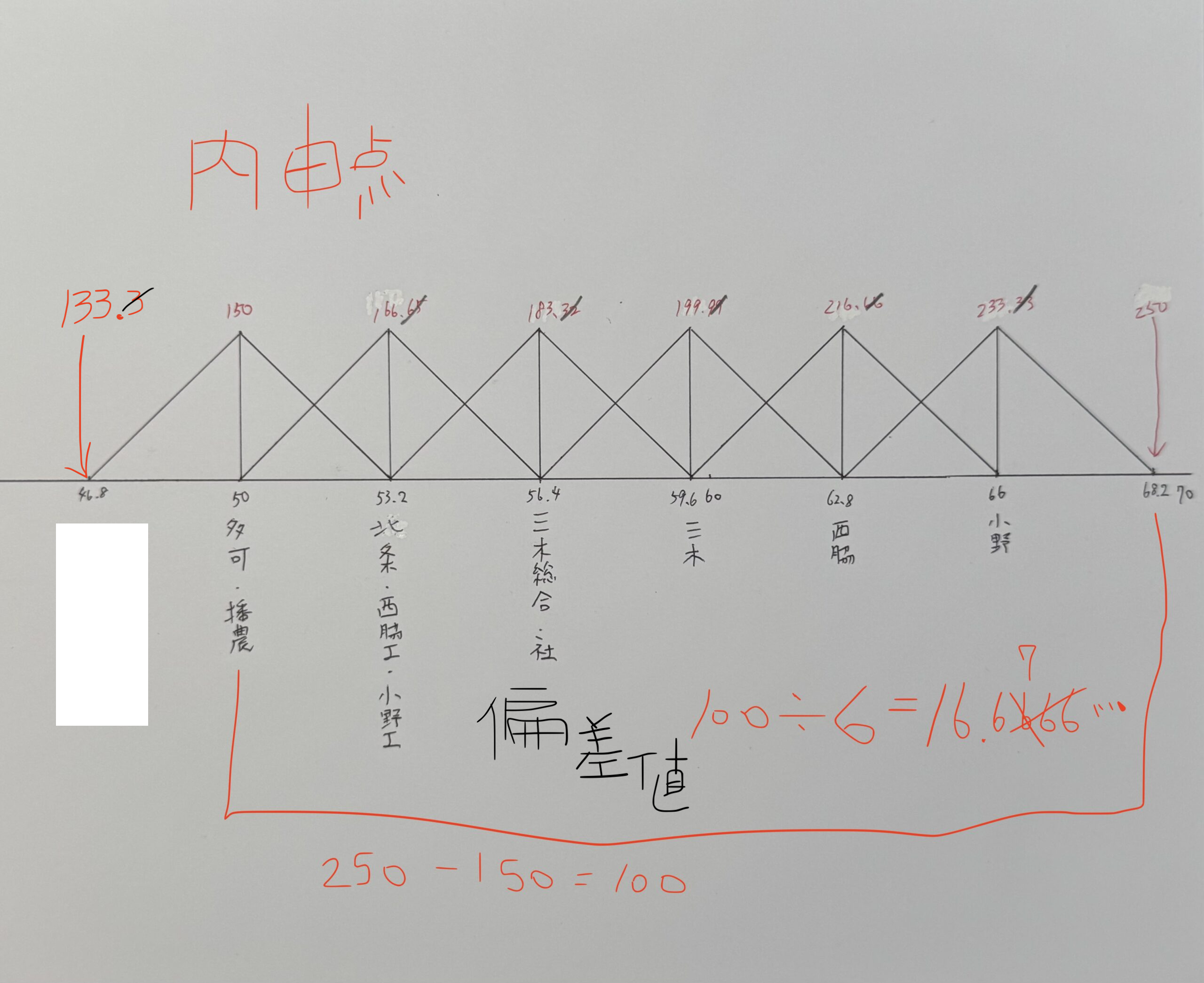
・兵庫県立小野高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立西脇高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立三木高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立三木総合高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立社高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立北条高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立西脇工業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立小野工業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立多可高等学校の偏差値と内申点と定員割れ状況をだしてみた。
・兵庫県立播磨農業高等学校の偏差値と内申点と定員割れ状況をだしてみた。
偏差値の算出方法（受験塾家庭教師による暫定）
内申点の算出方法（受験塾家庭教師による暫定）
・兵庫県公立高等学校【第3学区】明石市 加古川市 高砂市 西脇市 三木市 小野市 加西市 加東市 稲美町 播磨町 多可町
・【第3学区】加古川市や高砂市など各高校における偏差値と内申点と定員割れ状況
・【第3学区】明石市など各高校における偏差値と内申点と定員割れ状況
・【第3学区】小野市や三木市や西脇市や加東市や加西市など各高校における偏差値と内申点と定員割れ状況
・兵庫県公立高等学校（全日制・定時制・多部制・通信制）
・兵庫県にある各学区の各高校における偏差値と内申点と定員割れ状況
・直近のテストから志望校の合格最低点と自分の学力（偏差値と内申点）を知る。
・定員割れ公立高校の合格ラインは偏差値38で内申点80【兵庫県】
・過去10年分の定員割れ状況と兵庫県公立高等学校入学者選抜等
・複数志願選抜を知っとこ。【兵庫県公立高等学校入学者選抜より】
・兵庫県公立高等学校（定時制・多部制・通信制）の偏差値と内申点と定員割れ状況
・3年で卒業できる3修制がある兵庫県公立高等学校（定時制・多部制・通信制）
神戸市を拠点とする受験塾家庭教師オフィス神戸は【第3学区】に対応します。
三田市を拠点とする受験塾家庭教師オフィス三田は【第3学区】に対応します。
姫路市を拠点とする受験塾家庭教師オフィス姫路は【第3学区】に対応します。
加古川市を拠点とする受験塾家庭教師オフィス加古川は【第3学区】に対応します。
暫定的やけど例えば姫路にある高校の偏差値とか内申点とかを算出してみた。
基本的に「内申点が足らない」という状態で対応させて頂くのがほとんど。途中，志望校を変えない限りご契約当初にご提案させて頂く志望校へ合格してる。28年以上も。問い合わせ時点で，内申点が足らない足りる大事だ大事じゃない論争を繰り返されても，私的に弊社的に経験則から申し上げて「あまり気にしなくいいですよ！」というしかない。
【内申点（暫定）の求め方】
（基本的には令和7年度兵庫県公立高等学校入学者選抜要綱を参照）
先ずは第3学年1学期と第3学年2学期の通知表を準備する。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
例えば第3学年英語について考える。
3学年1学期「3」
3学年2学期「4」
よって（3＋4）÷2 ＝ 3.5
第3学年英語の評定を「3.5」と仮に定める。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
第3学年の評定を算出する。
① （数学＋英語＋理科＋社会＋国語）×4
② （音楽＋美術＋保健体育＋技術家庭）×7.5
以上より
内申点（暫定）＝ ①＋②
学校の夏休み課題を仕上げる。
数学については全ての問題に目を通します。英語についても同様，全ての問題に目を通します。それだけでなく全ての文章，全ての単語に目を通して一文，一文，一語，一語，ご本人様に合わせて抽出します。そのうえでご本人様のわからない，わかりにくい部分を掴み，「できる」に着地できるように結びます。
勉強するには時間が必要です。
「週34時間すべての時間を勉強に使いなさい！」ということではありません。「これだけ勉強時間があれば君が今，抱えている問題を早々に解決できるよ！」と励ますことができるので明確にしています。またその一方でご本人様の甘えから「忙しいから・・・」とする言い訳を排除する狙いがあったりもします。時間は財産です。その財産を如何に使用するか，で先の見通しを有意義に立てることができたりします。
