関西学院大学AO入試対策と甲南大学AO入試対策で,ダブル合格を達成!,合格に導く秘訣は,①親御様が『信じる心』をお持ちになられること,②ご本人様のオリジナリティーを大切にすること,③既成概念や主観に捉われず無いものを生み出すこと,④学校教師の「思ったこと、言いなり,余計なお世話」に疑問を持つこと,⑤過去問という視野で物事を立て付けないこと,これら5つです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーー
(3)学習指導教科
出願対策,小論対策,面接対策
(4)学習指導教材
大学資料,原稿用紙,その他
(5)学習指導内容
関西学院大学総合政策学部総合政策学科への志望に際し,AO入試に応じた対策(出願対策,小論対策,面接対策)を実施致します。
【志望】
関西学院大学総合政策学部総合政策学科
AO入試
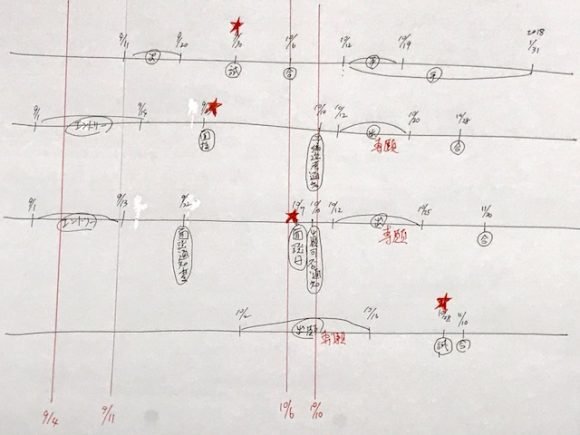
出願期間:2017年8月25日から2017年9月1日まで[志望理由書]
一次試験:2017年9月30日[小論]
一次合否:2017年10月6日
二次試験:2017年10月14日[面接]
二次合否:2017年10月20日
【出願対策】
上述を暫定とする大学における志望理由書の・・・・を状況如何に応じて対応致します。
【面接対策と小論対策】
両対策におきましては原則的に同時進行で行います。面接対策につきましては,志望動機における仕掛け原案を筆頭と致しまして各種内容(面接基本12テーマ,パーソナリティー,等その他)の対応原稿を制作し,その後,面接時間の割り振り作戦を実施致します。また,姿勢・発言・行動,といった言動練習も特訓致してまいりますので,その点では何卒ご安心頂ければ幸いに存じます。小論対策につきましては,当面の目標を40000字と致しまして,当日の試験で必ずしも対応しなければならない字数を鑑みたうえで,1テーマあたり400字ないしは800字に注力致します。現状の対応では,30分800字スキル,を暫定的と致しておりますが,当該志望校における字数におきまして,特にそこまで必要視することは,現時点で多少リスクを伴いますので,残された時間を勘案した結果,15分400字スキルを身に付けるかたちで当該対策を進めることもまたございます。なおテーマについては当該志望校における過去問を根幹としたうえで,各種社会的事由を盛り込んだものとする予定です。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーー
(3)学習指導教科
出願対策,小論対策,面接対策
(4)学習指導教材
大学資料,原稿用紙,その他
(5)学習指導内容
甲南大学マネジメント創造学部マネジメント創造学科への志望に際し,AO入試に応じた対策(出願対策,小論対策,面接対策)を実施致します。
【志望】
甲南大学マネジメント創造学部マネジメント創造学科
AO入試
出願期間:2017年9月1日から2017年9月6日まで[志望理由書・パーソナリティー]
一次合否:2017年9月22日
出願期間:2017年9月25日から2017年9月28日まで
二次試験:2017年10月7日[面接・グループワーク]
二次合否:2017年10月13日
【出願対策】
上述を暫定とする大学における志望理由書ならびにパーソナリティーの・・・・を状況如何に応じて対応致します。加えて論文(・・・・・)の使用を適用します。
【面接対策と小論対策】
関西学院大学総合政策学部総合政策学科AO対策に準ずることを原則として,捕捉する策を呈する。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーー