合格は勿論のこと,奨学金も入れたい!,という攻めた入試対策として,入試一ヶ月前から弊社スタッフが丹精込めて作ってくれました。スタッフいわく『長い間,本当に本当に良くして頂いたので私からの気持ちですm(_ _)m』ってこの短期間にこの量はヤバイなぁ!,受験塾家庭教師は受験塾家庭教師らしく謙虚で慎ましく,そして力強く支えましょッ(笑)


合格は勿論のこと,奨学金も入れたい!,という攻めた入試対策として,入試一ヶ月前から弊社スタッフが丹精込めて作ってくれました。スタッフいわく『長い間,本当に本当に良くして頂いたので私からの気持ちですm(_ _)m』ってこの短期間にこの量はヤバイなぁ!,受験塾家庭教師は受験塾家庭教師らしく謙虚で慎ましく,そして力強く支えましょッ(笑)


紆余曲折を経ながら一つ一つ取り組んでおります。また来年に向けて大学受験対策も一つ一つ丁寧に取り組んでおります!,時が経つのは本当に早いものです。この調子で2年生オール5を目指します。ちなみに1年生オール5でした。総合型選抜ならびに学校推薦型選抜ではとんでもない効果を発揮すること100%!
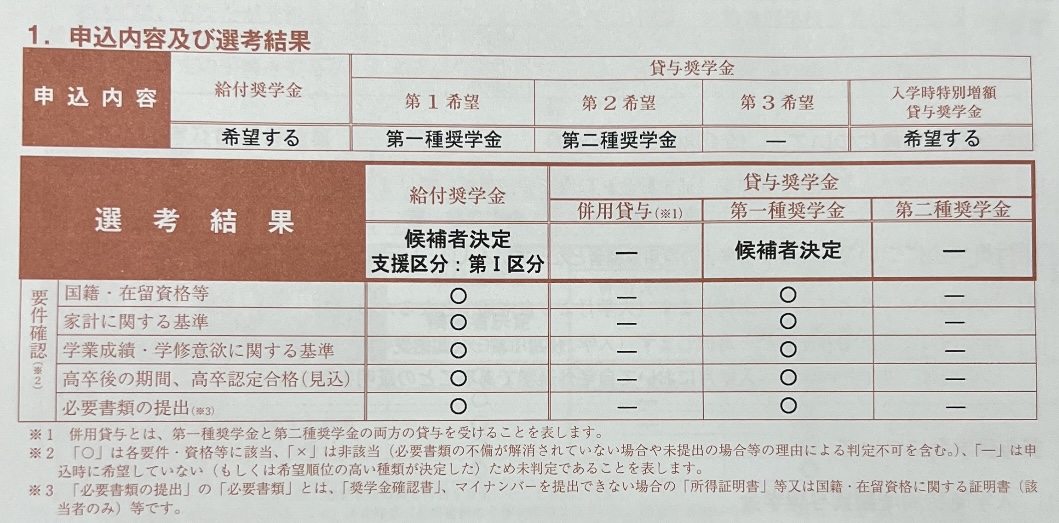
また一人お客様のお役に立つことができました。『これで息子が大学へいける!!!,先生のおかげや!!!』と喜んで頂けました。このご時世こういう事は本当に助かるので率先して,ご相談させて頂いております。なお採用区分については第I区分。安堵の表情を浮かべておられたので本当に良かったですww
ーーーーーーーーーーーーーーーーーーーーーー
「私立大学で自宅から通う」という状況で
第I区分に採用されていると,
① 年間授業料 ¥700,000減免
② 年間給付金 ¥459,600支給
③ 入学金260,000免除減額
ということが受けられる。
例えば
入学金260,000で年間授業料が1,200,000だとすると
実際にご家庭から支払う金額として
入学金¥0となり年間授業料¥40,400となる。
こういうことを知らない人達が多すぎるので,
私は率先してアドバイスさせて頂いています。
“即日翌日”を原則として何事も対応しております。
11/02木曜日に打ち合わせ
(60分無料体験指導と60分無料進学相談)
↓
11/03金曜日にご提案書作成
(文字数15039字のものを準備)
↓
11/04土曜日に速達郵送
(早ければ即日,遅くても週明け月曜日に到着)
↓
・ご了承または再考の場合はご連絡ください。
・特にそうでない場合はご連絡は不要です。




地域に育てられてる気がする!,三井住友銀行三田支店様に感謝感激致しておりますm(_ _)m。我が子は受験生と言えども指定校推薦入試を受けます。ほぼほぼ約束された入試なのだが,現時点でハッキリと合格が決まったわけでもないので,まだまだ緊張感がある。合格祈願に報えるように頑張ってもらいたい!

7,8ヶ月ぐらいかけて仕上げた。原稿用紙でいうところの146枚ちょっとあるみたい。これでまた一つ入試で使える武器ができたわけだ。知る人ぞ知る和田的”要約”ってことで,ココに過去問と一問一答問題集を重ねると共通試験で9割を超える得点率の確保が見込まれる。お客様にとっては料金の節約に繋がる!


現状の単位確保状況では,論理国語9/12,日本史探究8/9,数学Ⅱ11/12,数学B6/6,化学基礎5/6,生物基礎4/6,体育Ⅱ2/3,保健4/6,美術Ⅰ4/6,英語コミュニケーション9/12,家庭総合7/8,総合的な探究の時間Ⅱ0/1,キャリアガイダンス0/1,以上88カテゴリ中,69カテゴリを仕上げており,進級単位数として78.4%をクリアーできております。
<2023年10月度ご報告書より一部抜粋>

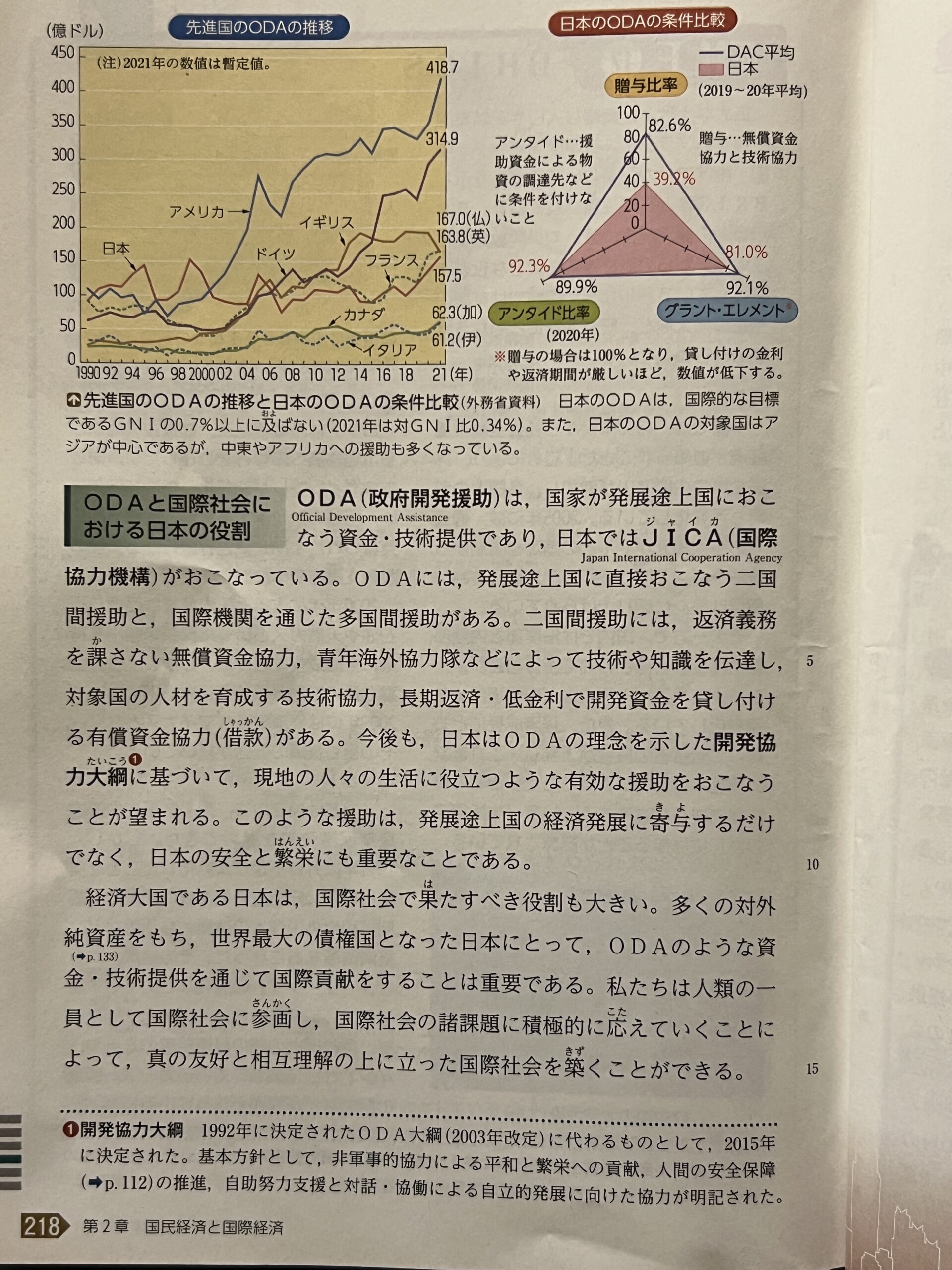
ODA
政府開発援助
国家が発展途上国におこなう資金・技術提供
日本ではJICA(国際協力機構)が行っている。
二国間援助と多国間援助がある。
二国間援助
返済義務を課さない無償資金協力
対象国の人材を育成する技術協力
開発資金を貸し付ける有償資金協力(借款)
開発協力大網に基づく。
開発協力大網
1992年に決定されたODA大網に代わるもの。
2015年に決定された。
非軍事的協力による平和と繁栄への貢献
人間の安全保障の推進
自助努力支援と対話・協働による自立的発展に向けた協力