カテゴリー: 17.中学生諸君へ

（1）令和4年度兵庫県公立高等学入学者選抜に向けて
https://www.hyogo-c.ed.jp/~koko-bo/02nyuushi/r4senbatu/r4senbatu.html

（2）兵庫県三田市の中学校3年生の人数＜例年5月31日付け＞

2021年：912人
2020年：929人
2019年：814人
2018年：918人
2017年：996人
2016年：1014人
2015年：1153人

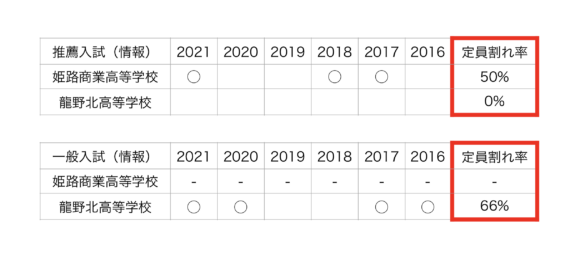
（3）2021兵庫県・公立高校・推薦入試・倍率1.0倍以下・定員割れ
https://www.jyukenjyuku.jp/blog/?p=56082

氷上高等学校・生産ビジネス
篠山東雲高等学校・地域農業
篠山産業高等学校・農と食
篠山産業高等学校・機械工学
篠山産業高等学校・電気建設工学
宝塚西高等学校・国際文化系
篠山鳳鳴高等学校・自然科学系
北摂三田高等学校・普通

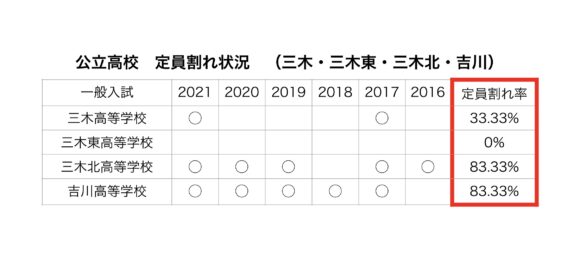
（4）2021兵庫県・公立高校・一般入試・倍率1.0倍以下・定員割れ
https://www.jyukenjyuku.jp/blog/?p=56095

宝塚高等学校
宝塚東高等学校
宝塚北高等学校
篠山鳳鳴高等学校
西宮今津高等学校
有馬高等学校・総合
氷上高等学校・生産ビジネス
氷上高等学校・食品ビジネス
氷上高等学校・生活ビジネス
篠山東雲高等学校・地域農業
篠山産業高等学校・農と食
篠山産業高等学校・機械工学
篠山産業高等学校・電気建設工学
篠山産業高等学校・総合ビジネス

（5）2021兵庫県・公立高校・推薦入試・三田市近辺の高校での定員と志願者数

北摂三田高等学校・普通
定員40名　志願者数46名

三田祥雲館高等学校・普通
定員100名　志願者数140名

三田西陵高等学校・普通
定員40名　志願者数57名

有馬高等学校・総合学科
定員100名　志願者数101名

有馬高等学校・人と自然科
定員20名　志願者数31名

（6）2021兵庫県・公立高校・一般入試・三田市近辺の高校での定員と志願者数

北摂三田高等学校・普通
定員164名　志願者数183名

三田祥雲館高等学校・普通
定員100名　志願者数142名

三田西陵高等学校・普通
定員160名　志願者数166名

有馬高等学校・総合学科
定員100名　志願者数88名

有馬高等学校・人と自然科
定員20名　志願者数28名

一見すると，姫路商業を推薦，龍野北を一般，という戦略で物事を立て付けるべきものと理解し易い。しかしそう簡単なものではない。受験には必ず「人」が関わるからだ。これは理解すべきだろう。そうすると自ずと大切にしなければならないものが志望動機。書面や口頭如何に関わらず心の準備が必要です。

時にご予算の都合上，未対応科目があったりする。対応している科目について比較的Goodな状況は続きます。ただ一方で未対応科目については未対応であるが故に，あまりGoodではない止むを得ない状況がどうしても続いてしまいます。入試直前になろうものなら，未対応だからこそ起きる不安感がやはり発出してしまいます。

「そんな時，どうするのか？」

過去問を通して，未対応科目の実態を探ってみます。対応科目の時間を活用するので，一発勝負。その背景から本来の対応科目への対応は一時的に停止してしまいます。ただ遅れが生じないように手元で工夫し，時間を捻出する中で活用しますので，未対応科目におけるリスクを考えると，そのリスクは分散されます。

◯は定員割れ。無記名は定員溢れです。ご参考までに！，「公立高校なら何処でもいい」とする気持ちがある場合，三木北か吉川を選んだうえで静かに勉強し，頭一つ飛び抜ければ合格容易いものと考えられます。戦略的に対応することで周囲との差を広げてみてはいかがでしょうか？！，意外と上手くいきますw

1.5時間でここまでイケた。二次関数を教えるついでに一次関数も教えてみた。めちゃくちゃ助かったらしく，重宝された。ま〜フツーやけど。宿題オンパレードってことで宜しく！，ちなみにこの夏，手元にある二次方程式の文章題も全部写して全部解けるようにしてみた。学力が身に付くってサイコーーッ！

【 二次関数（一次関数） 】

【 二次方程式の文章題 】

1ページ1題を基本とする。文章を写す。しきり線を引き上段（問題の文章）と下段（解くスペース）に分ける。下段についてはマス目を気にせず自由に書き込む。図やグラフがあれば書き，とにかく解くための手掛かりを模索する。その中で，ヒラメキや気付きがあれば手を動かす。整式を立てることができれば，キチンと解く。解けたら回答をキチンと表示する。答え合わせして正解していたら「◯」をつける。不正解ならば「×」をつける。ここで注意！，「×」の時，解説を書きたがる人達がいるけれど，そんな事をしちゃダメ。「×」だけで十分。以後ひたすら考え直し，正解となるまで再び解く行動に没頭する。最終的に「◯」となれば，それでクリアー。できない自分ができる自分になる瞬間です。